The Fractal Dimension model measures the complexity of a 2-dimensional structure by calculating its box-counting dimension [1]. This concept has been applied in oncologic studies for assessing the heterogeneity of tissue kinetics [2].
Operational Equation
The idea is to subdivide the area under the tissue TAC into a number of square boxes and simply count the number of boxes containing some part of the structure. The mesh size is defined as s, so 1/s gives the number of segments in each of the 2 dimensions. For instance, specifying 1/s=5 therefore means a subdivision into 5*5=25 boxes.
The counting process is performed with increasing number of intervals up to the specified 1/s. Next, the data are plotted in a double-logarithmic way, namely log(N(s)) on the y axis and log(1/s) on the x-axis.
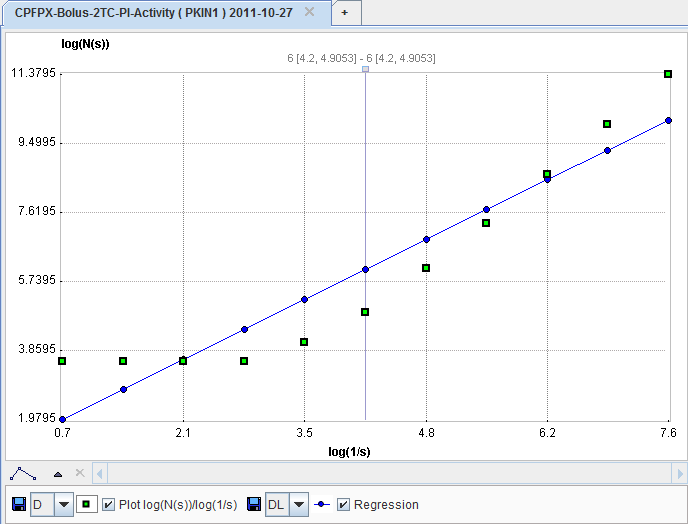
The box-counting dimension is finally obtained as the slope of a linear regression through the plotted points.
Implementation
After switching to the Fractal dimension model, two input parameters are available for specifying the box-counting process: 1/s, and Maximal value the highest TAC value which might occur in the data.
References
1.Peitgen H-O, Jürgens H, Saupe D: Chaos and fractals : new frontiers of science. New York: Springer-Verlag; 1992.
2.Strauss LG, Dimitrakopoulou-Strauss A, Koczan D, Bernd L, Haberkorn U, Ewerbeck V, Thiesen HJ: 18F-FDG kinetics and gene expression in giant cell tumors. J Nucl Med 2004, 45(9):1528-1535.